Орбитальная механика и законы Кеплера

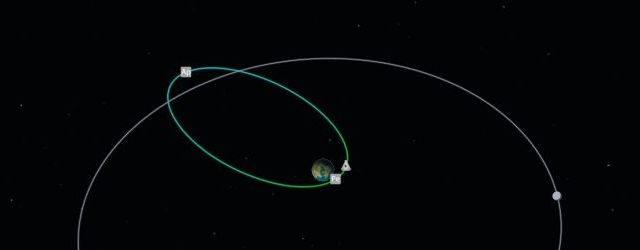
Не пугайтесь, друзья, в заметке не будет формул и сложной математики. Я постараюсь в доступной форме изложить основы орбитального движения, чтобы в следующий раз на примерах из игры рассказать о маневрировании на орбите.

Иоганн Кеплер сформулировал свои эмпирические законы планетарного движения в начале XVII-го века, проанализировав записи наблюдений другого великого астронома, Тихо Браге. Это была смелая для своего времени работа, поскольку она оспаривала казавшиеся незыблемыми постулаты теорий Аристотеля, Птолемея и Коперника.

Почти век спустя Ньютон доказал утверждения Кеплера в рамках своей теории всемирного тяготения. Законы Кеплера применимы к системам звезда-планета или планета-спутник, то есть тем, где одно из тел имеет значительно большую массу, чем другое.

За точными определениями, формулами и доказательствами — прошу в википедию.

Закон эллипсов — первый закон Кеплера

Каждая планета Солнечной системы обращается по эллипсу, в одном из фокусов которого находится Солнце.

Все знают, что эллипс — это такая сплющенная окружность. Геометрически эллипс можно построить имея карандаш, две булавки и завязанную в кольцо нитку.


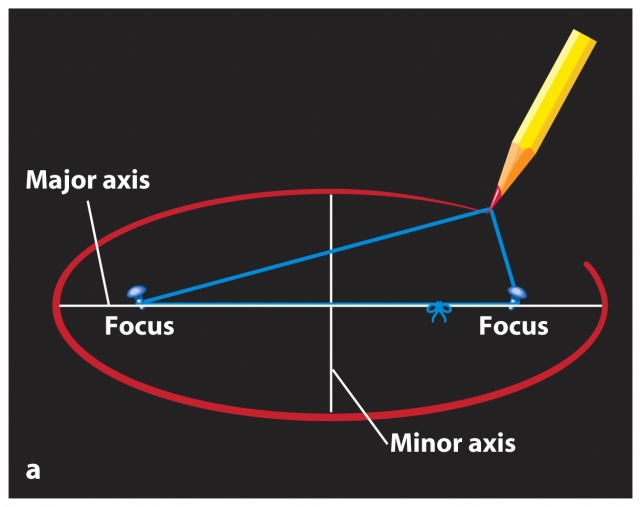
Булавки отмечают те самые фокусы, а нить позволяет выполнить условие определения эллипса: сумма расстояний до фокусов в каждой его точке постоянна.

Если Солнце находится в одном из фокусов, очевидно, что в разных точках орбиты планета будет на разном расстоянии от него.


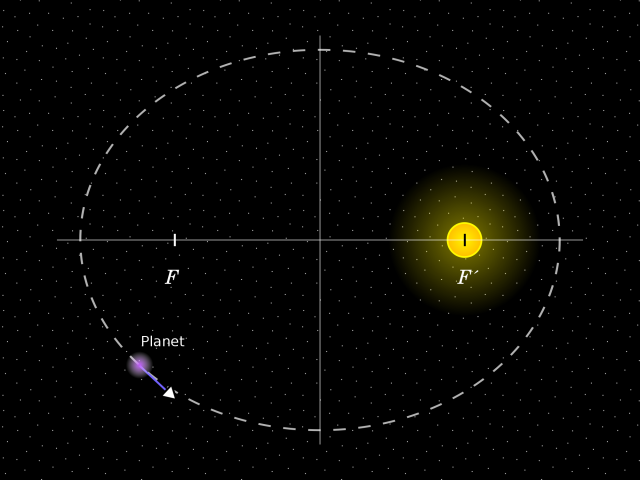
Самая близкая к центральному телу точка орбиты называется перицентр, а самая дальняя — апоцентр. Названия точек принято изменять в соответствии с именем центрального тела: у орбит вокруг Солнца — перигелий и афелий, у Земли — перигей и апогей, у Кербина — перикербин и апокербин, и так далее. В игре эти точки орбиты отмечены маркерами Periapsis (Pe) и Apoapsis (Ap).

Из-за того, что чаще всего обсуждают орбиты спутников Земли (ведь мы помним, что для них законы Кеплера также справедливы), в обычной речи перигей и апогей стали синонимами перицентра и апоцентра. Я тоже буду пользоваться этими привычными словами в своих рассказах.

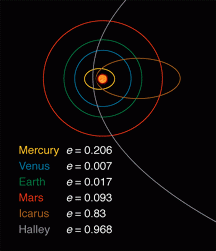
Внимание, сейчас нужно чуть-чуть напрячься. Центр эллипса лежит точно между фокусами. Самый маленький и самый большой радиусы, проведённые из центра — это малая и большая полуось эллипса (см. на картинке «Как нарисовать эллипс» выше). Вытянутость эллипса характеризует эксцентриситет — отношение половины межфокусного расстояния к большой полуоси. Чем он больше, тем более вытянут эллипс. Кстати, подумайте, какие фигуры получаются при e=0, e=1 и e>1. Можно расслабляться

Закон площадей — второй закон Кеплера

Каждая планета движется в плоскости, проходящей через центр Солнца, причём за равные промежутки времени радиус-вектор, соединяющий Солнце и планету, описывает равные площади.

Страшно звучит, правда? Если прохождение плоскости орбиты через центр притяжения интуитивно понятно, то радиус-векторы и площади… Давайте разбираться.


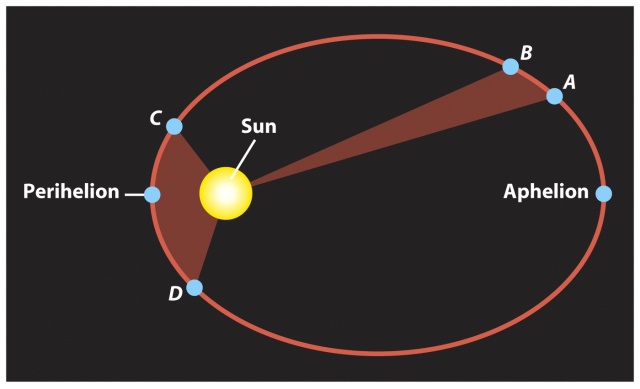
Если провести линию, соединяющую Солнце и планету, при движении по орбите она будет «закрашивать» некий сектор. Так вот, за одинаковые промежутки времени площадь такого сектора будет одинаковой, независимо от положения планеты.

Это означает, что на разных участках орбиты планета (или спутник) движется с разной скоростью! Действительно, все кербонавты знают, что в апогее скорость минимальна, а в перигее корабль разгоняется. Чем более вытянута орбита, тем больше разница скоростей. Только на идеально круглой орбите скорость везде одинакова.


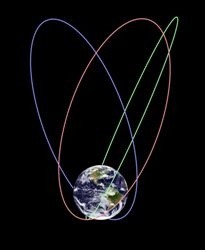
Это свойство используется, например, в реальной системе связи «Молния». Её спутники находятся на сильно вытянутых орбитах и большую часть времени проводят на пути к апогею или от него. Они обеспечивают связь над заданным участком планеты, а в перигее очень быстро проносятся с противоположной стороны и снова возвращаются в нужное положение.

Свой третий закон Кеплер вывел спустя почти десять лет после первых двух, и, по стечению обстоятельств, он имеет меньшее практическое значение для нас, кербонавтов. Если вы устали, можно его пропустить.

Гармонический закон — третий закон Кеплера

Квадраты периодов обращения планет вокруг Солнца относятся, как кубы больших полуосей их орбит.

Это простая пропорция говорит нам, что чем дальше планета находится от Солнца, тем медленнее она совершает полный оборот вокруг него. По соотношению можно, зная некоторые параметры орбит, определить неизвестные.


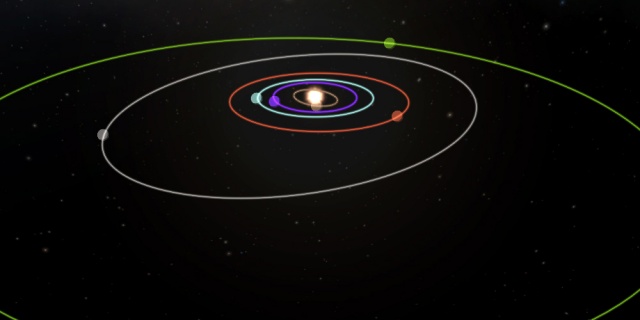
Ньютон уточнил эту закономерность, введя в неё массы планет. Благодаря этому можно определять массы удалённых небесных тел по данным астрономических наблюдений. Ну а сейчас вместо нас расчёты характеристик орбит планет, спутников и межпланетных кораблей может проводить компьютер.

В следующий раз мы начнём обсуждать другие орбитальные параметры и космические манёвры.

Продолжение следует…