Орбитальная механика и базовые манёвры

Сегодня в нашем космическом кружке мы рассмотрим орбитальные элементы и основные манёвры. Должен предупредить: в этот раз напрягать извилины придётся сильнее, так что не принимайтесь за чтение, если не готовы или устали. Инструменты KSP позволяют неплохо рисовать орбиты, так что большинство иллюстраций будет прямо из игры. Поехали!

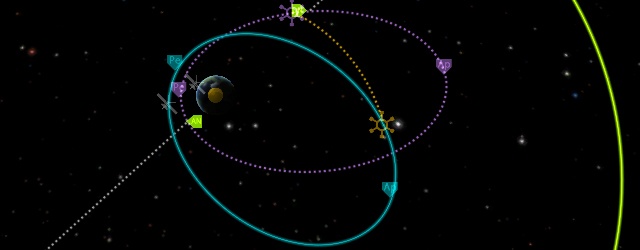
В прошлый раз мы разобрали законы Кеплера и помним, что планеты, их спутники и космические аппараты движутся по эллиптическим траекториям. Самая близкая к центру притяжения точка орбиты — это перигей, а самая удалённая — апогей. Они отмечены маркерами Ap и Pe. Плоскость, в которой лежит эллипс — это плоскость орбиты, и она всегда проходит через центр планеты или звезды, вокруг которой обращается корабль.


В Kerbal Space Program не рассматриваются случаи взаимодействия небесных тел сравнимой массы и вообще одновременное действие нескольких источников гравитации. Поэтому такие интересные вещи, как системы двойных звёзд или влияние планет-гигантов остаются за кадром.

Наклонение и узлы

Одной из важнейших характеристик орбиты является её наклонение (Inclination). Величину наклонения орбит спутников договорились отсчитывать от экваториальной плоскости планеты. Таким образом, это угол между плоскостью орбиты и плоскостью экватора. Для планет Солнечной системы наклонение отсчитывается от плоскости орбиты Земли, которая называется эклиптика. Например, орбита нашей Луны наклонена по отношению к экваториальной плоскости Земли примерно на 5°, а сам экватор наклонён к плоскости эклиптики на ~23°.


Кербину «повезло». Плоскость его экватора совпадает с плоскостью эклиптики (i=0°). Более того, главный космодром Кербина располагается точно на экваторе планеты, что позволяет запускать ракеты на орбиты с любым наклонением. Мы же пока не можем таким похвастать, например, знаменитый мыс Канаверал расположен на широте 28°N, а Байконур и вовсе на 46°N. Подумайте, какого минимального наклона орбиты можно достичь при запуске из этих точек?

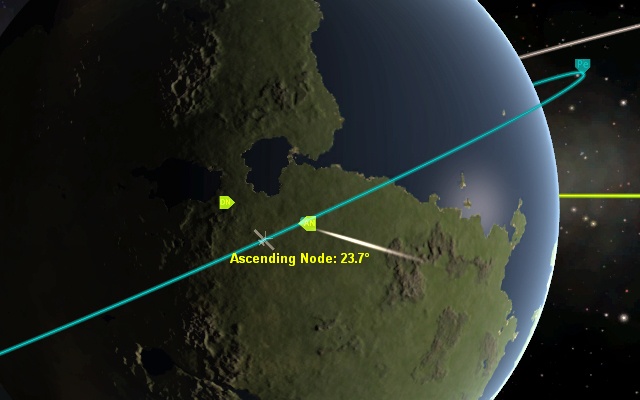
Точки пересечения орбиты с плоскостями экватора, эклиптики или других орбит называются узлы. Давайте разберемся на примере экваториальной плоскости Кербина. В игре её можно увидеть, «прицелившись» в Мун — оказывается, его орбита также имеет нулевое наклонение и совпадает с плоскостью экватора. Точка, в которой космолёт пересекает экватор с юга на север называется восходящий узел (Ascending Node, AN), с севера на юг — нисходящий узел (Descending Node, DN). Линия, соединяющая узлы, всегда проходит через центр притяжения.

Базовые манёвры и дельта-V

Каждому начинающему кербонавту необходимо осознать — на орбите нельзя резко сменить направление движения. Представьте, что вы несётесь по обледеневшей дороге со скоростью семь тысяч километров в час — повернуть или затормозить будет непросто. Однако, есть и обратная сторона. Любое, даже самое кратковременное, включение двигателей приведёт к изменению орбитальной траектории. Не здесь и сейчас, но где-то в другой части орбиты.

«Усилие», которое нужно приложить для изменения орбиты характеризуется величиной ΔV. Она показывает, на сколько нужно изменить скорость космического аппарата, чтобы перейти с одной траектории на другую. Манёвры с использованием двигателей можно разделить на "импульсные" и "не-импульсные". Эти определения не имеют отношения к физическому понятию импульса, а характеризуют продолжительность приложения движущей силы.

Импульсный манёвр — это математическая модель, подразумевающая мгновенное изменение скорости космического аппарата в заданной точке орбиты. Понятно, что в реальности соблюсти это условие невозможно, ведь двигатели имеют ограниченную тягу, но в космических масштабах погрешность будет невелика. Её можно свести к минимуму, зная время, необходимое для нужного изменения скорости.


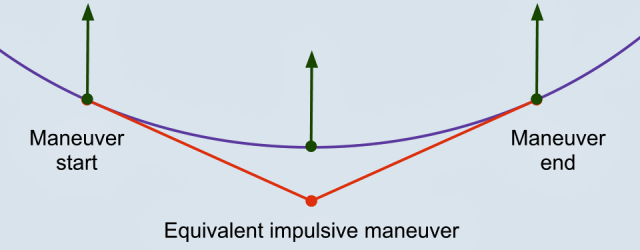
Не-импульсный манёвр подразумевает работу двигателя с низкой тягой продолжительное время и его расчёт требует информации о многих параметрах космического аппарата. В орбитальном планировщике KSP вычисления проводятся пока только по модели импульсных манёвров и пилотирование специфических кораблей с малой тягой, например, на ионных двигателях, требует дополнительного «раскидывания мозгами».

Помимо непосредственного значения ΔV нужно знать, в какую сторону его направить. В зависимости от направления приложения силы результат изменения орбиты будет различным.


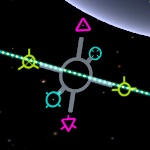
В системе координат орбитальных манёвров три главные оси:

1. Ось движения, направленная по касательной к орбите
2. Ось нормали, направленная перпендикулярно орбите
3. Ось радиуса, направленная к центру эллипса орбиты

На первый взгляд это кажется сложным. Давайте разбираться.

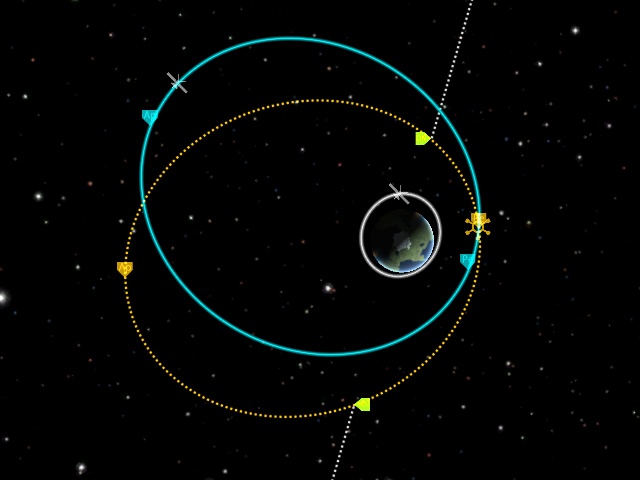
Большинство манёвров на орбите производится вдоль оси движения космического аппарата. Вектор, совпадающий с вектором скорости корабля называется прямым, а противоположный ему — обратным. В англоязычной среде этому соответствуют термины Prograde и Retrograde, которые часто просто транслитерируются. Направление прогрейда отмечено желтоватым кружком, а ретрогрейда — таким же кружком, но перечёркнутым. Эти же маркеры можно увидеть на navball'е.

Зажигания двигателей в прямом или обратном направлении непосредственно влияют на скорость корабля в данный момент и меняют перигей и апогей орбиты. Если разгоняться в перигее, апогей увеличится, а если тормозить — уменьшится. В апогее та же картина: если разгоняться, перигей поднимается, а если тормозить — опускается. Импульсы вдоль оси движения влияют на форму и ориентацию* орбиты и не изменяют её наклон.


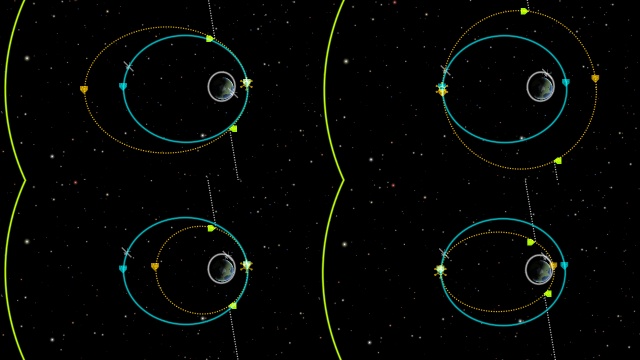
Перпендикулярная плоскости орбиты ось нормали отмечена треугольными пурпурными маркерами. Импульсы вдоль оси нормали влияют только на наклон орбиты и не изменяют ни её формы, ни ориентации*. При этом плоскость орбиты вращается вокруг прямой, соединяющей точку зажигания с центром притяжения. Представьте, что в момент совершения манёвра вы берёте длинную иголку и прикалываете свой корабль к центру планеты — вокруг этой неподвижной иглы и будет поворачиваться плоскость вашей орбиты.


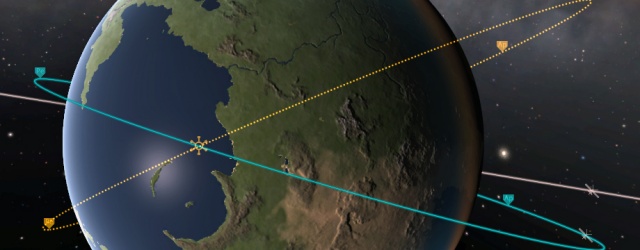
Третья, радиальная ось используется реже всего, но не менее важна. Она отмечена маркерами в виде синих кружков. Импульсы вдоль радиальной оси влияют на ориентацию* и форму орбиты в её плоскости, но не изменяют наклон. В разных точках траектории зажигания по радиальной оси имеют разные результаты, но, к сожалению, для рассмотрения этого в подробностях придётся написать заметку сравнимого объёма. Например, импульсы вблизи перигея приводят к развороту орбиты.



Давайте сейчас остановимся на этом. Теперь мы знаем, как совершать простые орбитальные манёвры, знаем, что такое дельта-V и как нужно зажигать, чтобы добиться желаемого. Мы готовы к тому, чтобы устроить встречу двух кораблей в космосе. О внутриигровом планировщике орбит и стыковке я расскажу в следующих обзорах интерфейса.