Перевод статьи из блога Мигеля Сеперо, в котором он рассказывает о трудностях перевода двумерной карты водоёма в трёхмерный вариант. procworld.blogspot.ru/2014/01/leveling-lakes.html
Этот пост продолжает повествование о воде.
Возможно вы захотите перечитать предыдущую заметку о воде. Мы закончили на создании двумерной булевой карты, где истина означает присутствие в этом месте воды. Неплохо, но нам ещё нужно решить противную проблемку — мы должны создать гладкий уровень воды в озёрах.
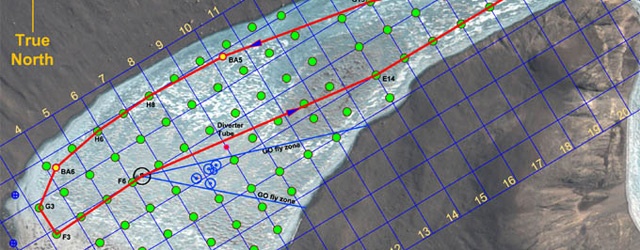
Будет проще, если мы взглянем на картинки. Представьте, что это участок, который нам нужно просчитать. Изначально он представляет из себя лишь карту высот и карту моря (в нашем случае это уровень моря):

А здесь видно фазу с расположением рек и озёр из прошлого поста. Они отмечены ярко розовым:
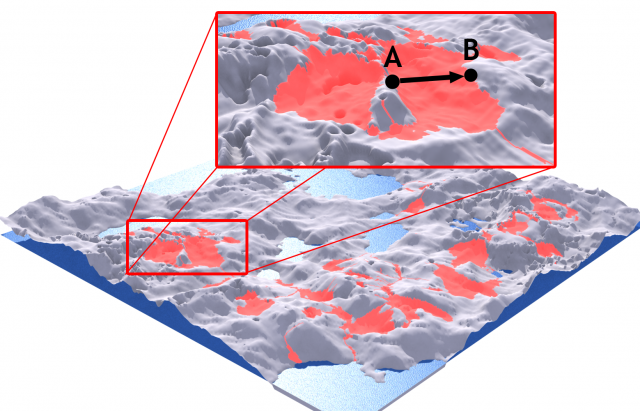
Как можно заметить на увеличенном фрагменте, часто озёра располагаются в очень сложном ландшафте. Нам известно, что береговые линии одного озера находятся на одной высоте. Проблема в том, чтобы вычислить уровень воды между А и В. Мы знаем, что путь А-В должен быть максимально плоским, это же касается пути из А в любую другую точку на границе берега, а таких потенциальных точек — масса.
Если бы мы обладали безграничным временем, можно было бы в первой фазе найти озёра, а потом выполнить своего рода повторяющееся выравнивание с помощью смягчения и/или фильтрации. Но у нас есть всего доля секунды на это, поэтому надо действовать по-другому.
Мы испробовали самые разные подходы. Большая часть из них была связана с растеризацией и интерполяцией, в первую очередь от берега к берегу, затем мы обратились за помощью к производным уровня воды. Ничего из этого не работало.
В последней очередной попытке мы попробовали подход, включающий в себя метод дерева квадрантов. Идея заключалась в том, чтоб закодировать водоёмы в квадродрева и применить те алгоритмы выравнивания, которые были бы слишком медленными, примени мы их на индивидуальных единицах воды.
Берега образовывали множество мелких квадратиков, но чем дальше от них, тем больше становились участки.
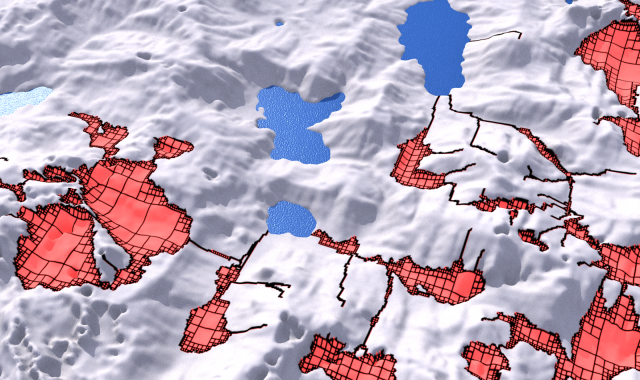
Можно заметить, что чем больше квадрат, тем более «обособлен» он от берега. Нам это понравилось. Мы могли поднимать или утапливать эти точки для того, чтоб получить необходимый нам уровень.
Как только уровень воды больших участков нас устроил, мы растеризовали его в карту высот воды. Это простая и быстрая билинейная интерполяция. Затем мы проделали то же самое с меньшими квадратами. Причина, по которой нужно обрабатывать сначала все квадраты заданного размера до того, как переходить к следующему уровню меньших, заключается в том, что для начала надо убедиться, что границы меньших участков совпадают с интерполированными значениями границ больших.
Полный процесс обсчёта достаточно быстр. На картинке ниже рендеринг найденных водоёмов. Он выглядит немного преувеличенным, но, думаю, вы поняли мысль.
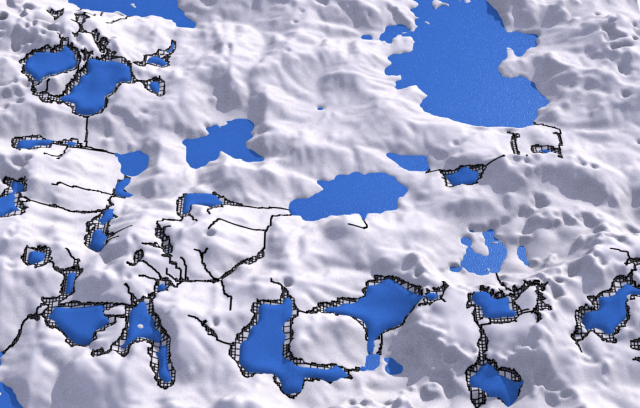
Нам ещё нужно поработать над эвристикой, но результат уже выглядит достаточно близко к тому, к чему мы стремимся.
Если из этого и можно вынести урок, то его можно сформулировать так: если вы в отчаянии, используйте квадродерево и всё будет в порядке.



14 комментариев
Просто таки гениально! :)
Если береговые линии находятся на одной высоте, то уровень воды между А и В = 0, но тогда и все эти вычисления не нужны. Возможно, тут тоже трудности перевода?)
В предыдущей статье это тоже было несколько неоднозначно:
Тоесть, как бы береговые линии всё же не на одной высоте и озеро таки течёт… но с другой стороны тут написано, что всё же не течёт)
Он не писал «горизонтальное», он писал именно «плоское». Но думаю, что разница действительно настолько невелика, что ей можно пренебречь.
А для воксельного движка полигон обычно сопоставим с размерами вокселя. Собственно и вся прелесть вокселей в том, что графическая часть уже работает по неким единообразным алгоритмам и про неё можно вообще забыть.
Если б разницей действительно можно было пренебречь, то достаточно было просто по булевой карте озера набросать колонны воды до уровня берега.
Опять же, будь оно плоским — то это была бы та же банальная интерполяция, о которой идёт речь в статье.
На сколько я понимаю, озёра тут не только не плоские, они чаще всего весьма выпуклые, как и показано в преувеличенном виде на последнем рисунке.
В предыдущей статье говорится, что озёра берутся из алгоритма просчёта рек, правда не вдаётся в подробности. Тоесть, проблема возникла скорее из-за приблизительного алгоритма составления самой булевой карты — которая дала в результате довольно кривые по высоте берега у озера. Их просто нельзя было простым способом интерполировать.
Это не воксельный движок в том виде, в котором ты подразумеваешь. Пройди по тэгу Voxel Farm, почитай.
Вода же в окончательном варианте, как я понял, будет состоять из т.н. «высоких вокселей», где есть всего несколько верхних слоёв обычных вокселей и один нижний неравномерный слой столбиков. Этот вариант довольно давно применяется и довольно шустрый, нежели если считать всё.
Дык об этом была как раз предыдущая статья, а это уже ведёт речь об алгоритме, использующему рассчитанные контуры озера.
С другой стороны ты прав, он строит не горизонтальное озеро, а как в реальной жизни — с течением, т.е. наклонное.
Но если у тебя вопросы технического характера, то лучше, конечно, обратиться к самому Мигелю за разъяснениями. Ссылка на его блог в статье указана. Можно ещё его найти в g+ под тем же именем.
Именно оптимизацией больше всего и занимается Мигель. Все предыдущие его посты были в основном как раз о графике. А вот например ими придуманный потрясающий метод гладкого перехода между LODами https://www.youtube.com/watch?v=rakmUDn7O_s