Machinations.io и экономика вокруг точильного камня

В игре заточка меча с первого на второй уровень стоит 10 золота и имеет шанс 90% (золото тратится, в случае неудачи меч не изменяется). Заточка со второго на третий уровень стоит 20 золота и имеет шанс 80% (золото тратится, в случае неудачи меч понижается на 1 уровень). Таким же образом меч можно улучшить с третьего до четвертого: заточка стоит 40 золота и имеет шанс 70%. И так далее (с каждым уровнем цена повышается в два раза, а шанс уменьшается на 10%). Золото тратится в любом случае при каждой попытке, в случае неудачи меч понижается на один уровень (но не ниже первого).

Рассчитайте среднюю стоимость улучшения меча до седьмого уровня.

«Заточка» игровых предметов — краеугольный камень геймдизайна традиционных ММО. Это и теоретически бесконечная самовоспроизводящаяся геймплейная петля, и неограниченный источник мотивации для игрока, гонящегося за самым лучшим снаряжением, и эффективный способ вывода излишков ресурсов из игровой экономики. Правильно отбалансировать количество итераций «заточки» предмета и объем затрачиваемых на него ресурсов — достаточно нетривиальная проблема. Приведенная выше задача не первый год кочует по около-геймдевным формумам и пабликам, а также встречается в реальных тестовых заданиях на должность геймдизайнера.

Самым правильным и традиционным решением данной задачи будет приведение ее к уравнению из теории вероятности. Теория вероятности — это раздел высшей математики. Высшая математика — это сложно. Высшая математика дается далеко не всем. Но как же быть тем, в чьей голове генерируются дюжины идей по построению взаимодействий между людьми и системой, между людьми и людьми, между людьми и уникальными, неповторимыми игровыми мирами? Есть ли шанс профессионально заниматься геймдизайном для тех, у кого одним из ключевых аргументов для поступления на факультет востоковедения было полное отсутствие математики как явления в программе обучения? Давайте обратим свой взгляд на Machinations.io Будем смотреть и разбираться.

Machinations.io — это профессиональный инструмент геймдизайнера для построения блок-схем игровых механик, прототипирования и простейшего визуального программирования. Этот инструмент не даст нам тех быстрых, четких и изящных ответов, какие могли бы предоставить выверенные формулы теорвера. Однако Machinations.io может предоставить в наше распоряжение кое-что более ценное для игродела — полноценный прототип работающей игровой механики «заточки» меча, сделанный на коленке за пять минут. По нему можно будет проследить весь тернистый путь меча к желанному седьмому уровню, на практике увидеть необходимое количество итераций, объем затраченных ресурсов, а затем масштабировать весь процесс на сколь угодно большое (в платной версии утилиты) количество мечей.

Для начала быстро взглянем, как устроен интерфейс утилиты:

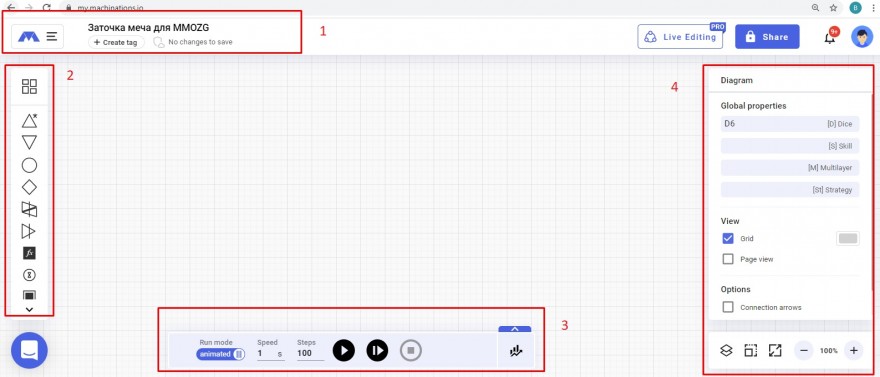
Главное рабочее пространство представляет собой линованный лист бумаги, хорошо знакомый всем, кто работает с инструментами для составления блок-схем, вроде Draw.io.

В поле 1 расположились привычные инструменты управления и заголовок нашего документа.
В поле 2 находятся все инструменты machinations.io
В поле 3 расположены инструменты управления ходом симуляции
В поле 4 находится меню настройки параметров выбранного элемента.

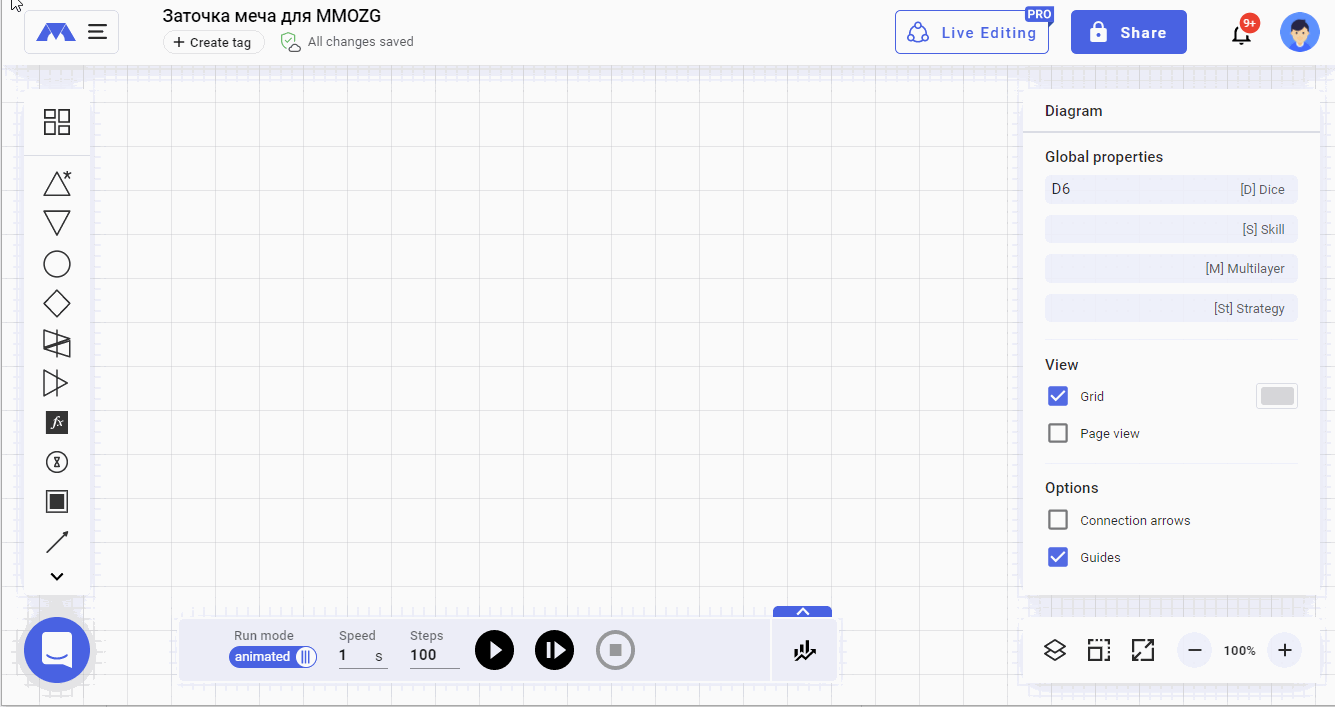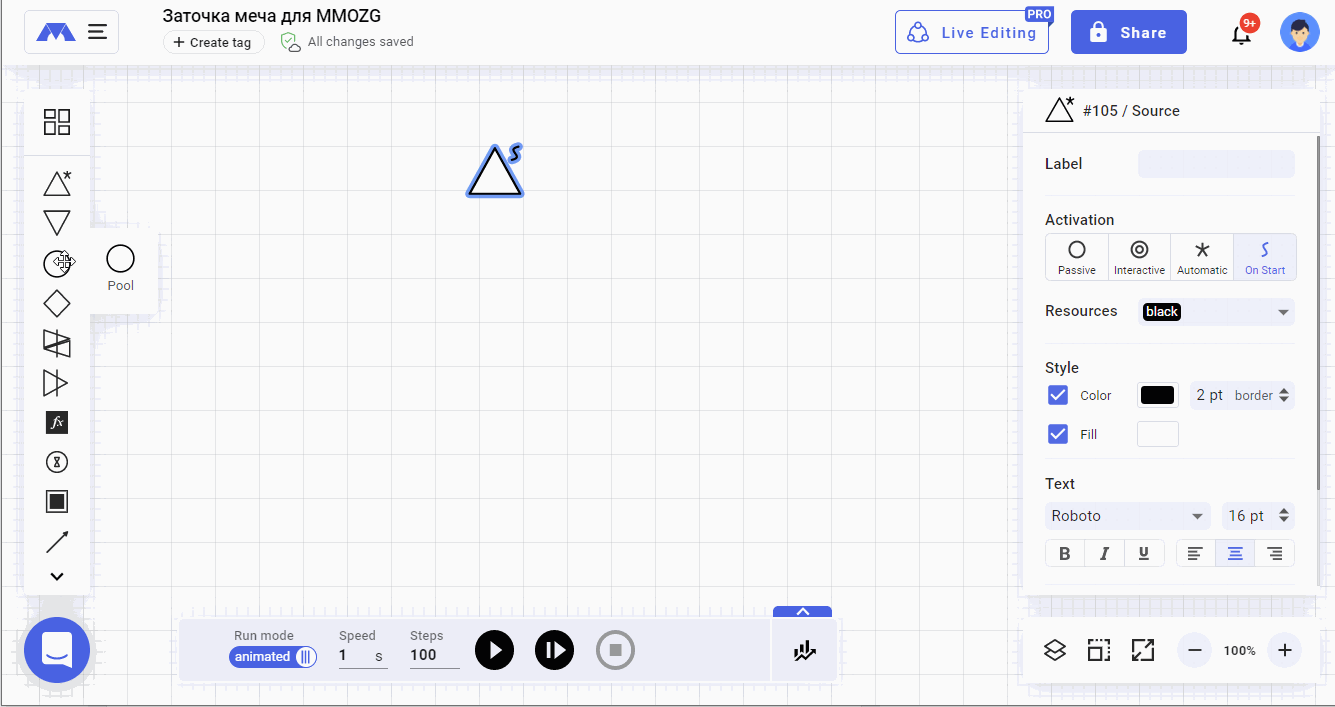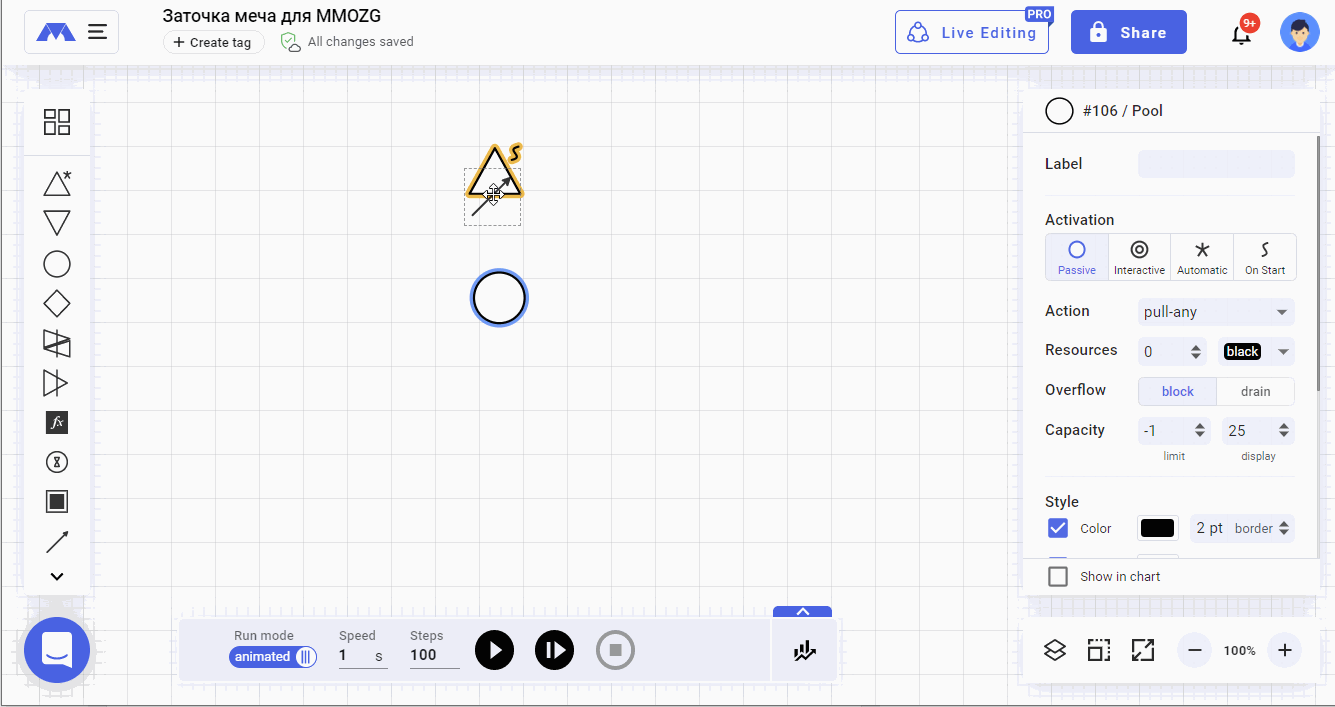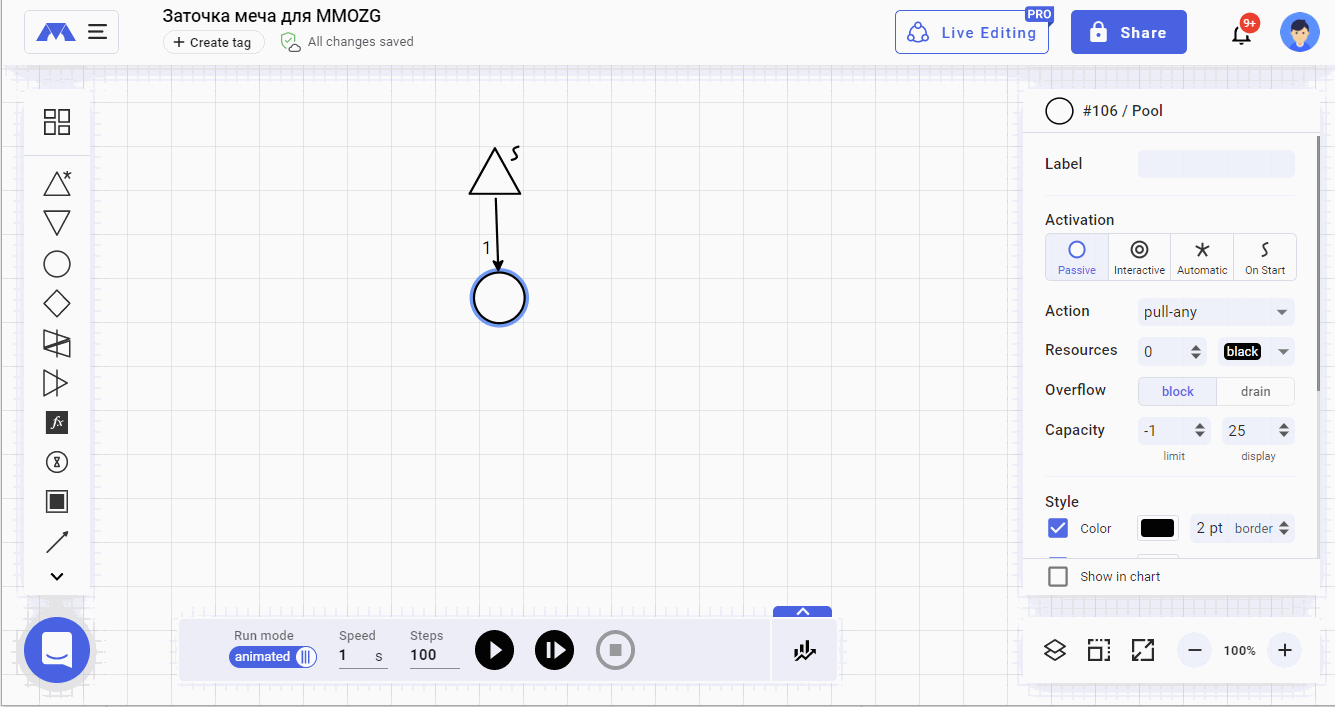
Начало начал любой игровой механики в machinations.io — это источник ресурса. В нашем случае ресурсом станет меч, который будет проходить итерации «заточки». Для того, чтобы в выстраиваемой нами системе мог появиться этот самый меч, мы берем из поля 2 элемент source (источник ресурса) и размещаем его на рабочем поле.

Для того, чтобы поступление мечей в механику было контролируемым, в поле 4 выставляем его свойство в значение OnStart. В таком положении источник выдаст нам один меч на старте симуляции и более не будет предпринимать никаких действий.

Следующим действием установим место, или если угодно — «инвентарь», куда поступит выданный нам меч.

Берем из поля 2 элемент pool и размещаем его на рабочем поле. От элемента source проводим дорожку к элементу pool.

Итак, первый минимально необходимый результат достигнут. При нажатии на кнопку воспроизведения симуляции, источник ресурса выдаст нам «меч, 1шт.» и передаст его в «инвентарь».

«Кликабельная» гифка с процессом.

Шаг 2 — это построение собственно итераций заточки меча. Тут начинаются основные хитрости.

Выбираем на боковой панели инструмент «Gate» (шлюз) и размещаем его на поле. Предназначение этого элемента — распределять ресурсы по развилкам дорожек. Наша задача — настроить его так, чтобы он брал «меч» 1 уровня, «подсчитывал» стоимость его заточки и с 90% вероятностью превращал его в «меч» 2 уровня.

Прокладываем дорожку из «инвентаря» с мечами 1 уровня к шлюзу. Затем заходим в параметры шлюза и выбираем там способ распределения — «случайный» (distribution — random). Из шлюза выводим 2 дорожки, на каждой из которых прописываем процентную вероятность того, что ресурс последует по ней. Как сказано в задаче — 90% шанс, что меч заточится до 2 уровня и 10% вероятности, что вернется обратно на 1 уровень. Важно понимать, что если забудем про дорожку с «провалом» заточки, то с 10% вероятностью наш «меч» просто испарится.

И третий важный трюк — научить схему считать стоимость заточки.

Располагаем на поле еще один источник ресурсов. Он будет генерировать стоимость в золотых монетах каждый раз, когда «меч» будет проходить через рандомизатор. Для этого устанавливаем свойства источника на «пассивные» (иначе он будет генерировать ресурсы по своему желанию) и подключаем его с помощью пунктирной стрелки state connection («соединение состояния») к рандомизатору. На стрелке указываем правило, согласно которому, как только на нашем импровизированном точильном камне количество мечей становится равным 1 (=1), источник золотых монет должен будет сгенерировать стоимость заточки, равной 10.

Вторая кликабельная гифка. На этом этапе уже можно нажать кнопку воспроизведения и посмотреть как занятно бегают по дорожкам схемы кружочки ресурсов и считаются циферки затрат.

Следующий этап конструирования симуляции во многом дублирует предыдущий. Главным отличием будет неудачный исход заточки. В случае провала, меч не вернется на 2 уровень, а откатится еще на 1 уровень вниз. Ну и стоимость заточки с каждым этапом возрастает, а шанс на успех — падает.

Растут ставки и количество задействованных элементов на схеме.

Так как по условиям задачи меч необходимо точить до 7 уровня, а алгоритм заточки начиная с предыдущего шага будет неизменным, вместо воспроизведения одного и того же шага еще 5 раз прибегнем к магии кропотливой и рутинной работы и достроим последовательность действий по уже отработанным лекалам за кадром.

Теперь нужно «научить» алгоритм логике действий в ситуациях, когда меч успешно наточен до 7 уровня и когда мечей накопилось столько, что можно подводить статистически достоверные итоги стоимости.

Первым делом, после заточки «меча» до 7 уровня, вместо привычного пула мы располагаем шлюз. В этот раз не рандомизирующий, а простой. Его задача — регистрировать прохождение ресурса и посылать сигнал новому сделанному нами источнику «мечей», что пора пускать в работу следующее изделие. Если не прибегать к такой сигнальной системе, а просто пускать в процесс заточки «мечи» непрерывно один за одним, то есть риск, что одновременно в одном рандомизаторе окажутся 2 меча, а стоимость «считается» только с одного.
И последним шагом мы задействуем элемент End Condition («Условие остановки»). Располагаем его на поле, а рядом с ним — пул с законченными изделиями. Пунктирная стрелка, соединяющая пул с «выключателем» подаст сигнал об остановке симуляции, когда будет готово 1000 «мечей».

Магия рутинной и кропотливой работы не только достроила за кадром схему до впечатляющих размеров, но и добавила цветовую кодировку, а также поясняющие надписи.
Кто заметит на гифке ошибку — тот молодец ;)

Ну что ж, все готово! Еще раз перепроверяем все шаги, настраиваем условия симуляции (скорость, количество шагов и прочее) и жмем на запуск!

«Мечи» точатся, «монеты» считаются. Кружочки бегают по дорожкам, задействованные условия и алгоритмы подсвечиваются и мигают. Любишь игры про автоматизацию? Оглянись вокруг! Разве здесь не прекрасно?

Для желающих все потрогать своими руками, вот финальный результат (может не дружить с браузерами помимо Google Chrome).

На мой вкус, такой вот практический подход к решению задач для геймдизайнеров гораздо веселее элегантного, но холодного теорвера. Расставлять по линованому полю шлюзы и пулы, соединять их дорожками и любоваться снующими по всей этой логистике ресурсами почти так же залипательно, как играть в Factorio. И это мы еще не трогали преобразователи и формулы! До них, возможно, доберемся в другой раз.